LeetCode 刷题记录
2024-09-02 11:37:40 # 算法题 #leetcode #算法

Leetcode

1. 两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

示例 1：

1
2
3
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

解题思路

1.暴力法

对两两数字和加起来进行比较

复杂度：

  • 时间复杂度：O(n^2)，n 为数组长度
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] ret = new int[2];
        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] + nums[j] == target) {
                    ret[0] = i;
                    ret[1] = j;
                }
            }
        }
        return ret;
    }
}

2.哈希表

对于数组中的每一个x要找到target - x时间复杂度是 O(n^2)，如果使用哈希表将数组中的每一个数保存下来，寻找target - x的时间复杂度就可以降到 O(1)

复杂度：

  • 时间复杂度：O(n)，n 为数组长度
  • 空间复杂度：O(n)，n 为数组长度

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(target - nums[i])) {
                return new int[]{i, map.get(target - nums[i])};
            }
            map.put(nums[i], i);
        }
        return new int[0];
    }
}

88. 合并两个有序数组

给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。

初始化 nums1 和 nums2 的元素数量分别为 m 和 n。你可以假设 nums1 的空间大小等于 m + n，这样它就有足够的空间保存来自 nums2 的元素。

示例 1：

1
2
输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]

解题思路

1.先合并，再排序

将nums2中的元素加入nums1，再对nums1排序

复杂度：

  • 时间复杂度：O( (m+n) log(m+n) )，快排的时间复杂度
  • 空间复杂度：O( log(m+n) )，快排的空间复杂度

参考代码

1
2
3
4
5
6
7
8
class solution{
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        for (int i = 0; i < n; i++) {
            nums1[m + i] = nums2[i];
        }
        Arrays.sort(nums1);
    }
}

2.双指针法

方法 1 没有用到题目中nums1和nums2有序的性质，可以用两个指针i、j分别指向nums1、nums2的下标，并根据下标进行比较，但是需要一个新数组保存结果

复杂度：

  • 时间复杂度：O(m + n)
  • 空间复杂度：O(m + n)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = 0;
        int j = 0;
        int[] sorted = new int[nums1.length];

        while (i < m && j < n) {
            if (nums1[i] < nums2[j]) {
                sorted[i + j] = nums1[i++];
            } else {
                sorted[i + j] = nums2[j++];
            }
        }

        if (i < m) {
            while (i < m) {
                sorted[i + j] = nums1[i++];
            }
        } else {
            while (j < n) {
                sorted[i + j] = nums2[j++];
            }
        }

        for (int k = 0; k < m + n; k++) {
            nums1[k] = sorted[k];
        }
    }
}

3.逆向双指针

方法 2 中新建了一个sorted数组保存排序结果，但是题目中nums1中已经预留了空间，所以可以从大的开始排序，并放入nums1的空闲区

复杂度：

  • 时间复杂度：O(m + n)
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m - 1;
        int j = n - 1;

        while (i >= 0 && j >= 0) {
            if (nums1[i] > nums2[j]) {
                nums1[i + j + 1] = nums1[i--];
            } else {
                nums1[i + j + 1] = nums2[j--];
            }
        }

        if (i > 0) {
            while (i >= 0) {
                nums1[i + j + 1] = nums1[i--];
            }
        } else {
            while (j >= 0) {
                nums1[i + j + 1] = nums2[j--];
            }
        }
    }
}

53. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：

1
2
3
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

解题思路

假设 dp[i]是以 nums[i]结尾的最大子序列和，则

最大子序列和 max 就是 dp 数组中的最大值

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
public int maxSubArray(int[] nums) {
	//dp[i]表示以nums[i]结尾的最大子序列和
	int[] dp = new int[nums.length];
	dp[0] = nums[0];
	int max = nums[0];

	for (int i = 1; i < nums.length; i++) {
		//以 nums[i] 结尾的最大子序列和 == 以 nums[i-1] 结尾的最大子序列和 + nums[i] 或者是 nums[i]
		dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);
		max = Math.max(dp[i], max);
	}
	return max;
}

26. 删除有序数组中的重复项

给你一个有序数组 nums ，请你** 原地** 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。

示例 1：

1
2
3
输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

解题思路

1.暴力法

对于nums[i]，找到第一个比nums[i]大的数放在nums[i+1]的位置，直到找不到比nums[i]还要大的数。最后返回i+1即数组的新长度

复杂度：

  • 时间复杂度：O(n^2)
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int removeDuplicates(int[] nums) {
        int len = nums.length;
        for (int i = 0; i < len - 1; i++) {
            for (int j = i + 1; j < len; j++) {
                if (nums[j] > nums[i]) {
                    nums[i + 1] = nums[j];
                    break;
                }
                if (j == len - 1) {
                    return i+1;
                }
            }
        }
        return len;
    }
}

2.双指针

如果存在nums[i] = nums[j]，则对于 $$i \leq k \leq j$$ 有nums[i] = nums[k] = nums[j]，即相等的元素下标一定连续。通过维护slow和fast快慢指针，可以将空间复杂度降低到 O(n)

复杂度：

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int removeDuplicates(int[] nums) {
        int slow = 0;
        int fast = slow + 1;
        while (fast < nums.length) {
            if (nums[slow] == nums[fast]) {
                do {
                    fast++;
                } while (fast < nums.length && nums[slow] == nums[fast]);
                if (fast == nums.length) {
                    break;
                }
                nums[slow+1] = nums[fast];
                slow++;
            } else {
                slow++;
                fast++;
            }
        }
        return slow + 1;
    }
}

双指针简易写法

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int removeDuplicates(int[] nums) {
        int i = 0;
        for (int j = 1; j < nums.length; j++) {
            if (nums[i] != nums[j]) {
                nums[++i] = nums[j];
            }
        }
        return ++i;
    }
}

350. 两个数组的交集 II

给定两个数组，编写一个函数来计算它们的交集。

示例 1：

1
2
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

解题思路

1.哈希表

对nums1和nums2创建两个哈希表map1和map2，以数组中出现的数字为 Key，出现的次数为 value，如果两个表存在相同的key值，则返回较小的value，此value就是两个数组中key的交集

复杂度

  • 时间复杂度：O(n + m)
  • 空间复杂度：O(n + m)

参考代码

(自己写的稀碎)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        Map<Integer, Integer> map1 = new HashMap<>();
        for (int i = 0; i < nums1.length; i++) {
            if (!map1.containsKey(nums1[i])) {
                map1.put(nums1[i], 1);
            } else {
                int count = map1.get(nums1[i]);
                count++;
                map1.put(nums1[i], count);
            }
        }

        Map<Integer, Integer> map2 = new HashMap<>();
        for (int i = 0; i < nums2.length; i++) {
            if (!map2.containsKey(nums2[i])) {
                map2.put(nums2[i], 1);
            } else {
                int count = map2.get(nums2[i]);
                count++;
                map2.put(nums2[i], count);
            }
        }

        List<Integer> ret = new ArrayList<>();
        Set<Integer> keySet = map1.keySet();
        for (Integer key : keySet) {
            if (map2.containsKey(key)) {
                int count = map1.get(key) > map2.get(key) ? map2.get(key) : map1.get(key);
                for (int i = 0; i < count; i++) {
                    ret.add(key);
                }
            }
        }

        int[] result = new int[ret.size()];
        int i = 0;
        for (Integer integer : ret) {
            result[i++] = integer;
        }
        return result;
    }
}

用较小的数组建哈希表降低空间复杂度

复杂度

  • 时间复杂度：O(n + m)
  • 空间复杂度：O($$min\lbrace n,m\rbrace$$)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        if (nums1.length > nums2.length) {
            return intersect(nums2,nums1);
        }

        Map<Integer, Integer> map = new HashMap<>();
        //map.getOrDefault(key, defaultValue) 如果存在key，返回key的value；如果不存在返回defaultValue
        for (int i : nums1) {
            int count = map.getOrDefault(i, 0) + 1;
            map.put(i, count);
        }

        int[] intersection = new int[nums1.length];
        int index = 0;
        for (int i : nums2) {
            int count = map.getOrDefault(i, 0);
            if (count > 0) {
                intersection[index++] = i;
                count--;
                if (count > 0) {
                    map.put(i,count);
                } else {
                    map.remove(i);
                }
            }
        }

        return Arrays.copyOfRange(intersection,0,index);
    }
}

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

1
2
3
4
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

解题思路

1.蛮力法（超出时间限制）

对第i天买入，计算之后每天的利润，并保存最大值。返回最后的最大值。

复杂度：

  • 时间复杂度：O(n^2)
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int maxProfit(int[] prices) {
        int max = 0;
        for (int i = 0; i < prices.length - 1; i++) {
            for (int j = i + 1; j < prices.length; j++) {
                if (prices[j] - prices[i] > max) {
                    max = prices[j] - prices[i];
                }
            }
        }

        return max;
    }
}

2.单调栈

维护一个单调栈

  • 入栈元素大于等于栈顶元素时，直接入栈
  • 入栈元素小于栈顶元素时，将栈顶弹出，并计算它与栈底元素的差值，直到找到一个元素小于等于入栈元素
  • 在数组最后设置一个哨兵，为了使栈中元素得到计算

第二条可以这样理解，栈顶元素为a，入栈元素为b，当b入栈时，之后入栈的元素C一定存在 $$C-b > C-a$$

此时a已经没用了，计算一下与利润即可弹出。

复杂度：

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int maxProfit(int[] prices) {
        Stack<Integer> stack = new Stack<>();

        stack.push(prices[0]);
        int low = prices[0];
        int max = 0;
        for (int i = 1; i < prices.length; i++) {
            if (stack.peek() < prices[i]) {
                stack.push(prices[i]);
            } else if (stack.size() == 1 && stack.peek() > prices[i]) {
                stack.pop();
                low = prices[i];
                stack.push(prices[i]);
            } else if (stack.peek() > prices[i]) {
                while (!stack.isEmpty() && stack.peek() > prices[i] ) {
                    Integer pop = stack.pop();
                    if (pop - low > max) max = pop - low;
                }
                stack.push(prices[i]);
                if (stack.size() == 1) low = stack.peek();
            }
        }
        while (stack.size() > 0) {
            Integer pop = stack.pop();
            if (pop - low > max) max = pop - low;
        }
        return max;
    }
}

3.一次遍历

第i天的最大收益是maxProfig = price[i] - minPrice，即第i天的价格减去第i天前的历史最低价。

复杂度：

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxProfit(int[] prices) {
        int minPrice = Integer.MAX_VALUE;
        int maxProfit = 0;

        for (int i = 0; i < prices.length; i++) {
            if (prices[i] < minPrice) {
                minPrice = prices[i];
            } else if (prices[i] - minPrice > maxProfit) {
                maxProfit = prices[i] - minPrice;
            }
        }

        return maxProfit;
    }
}

566. 重塑矩阵

给出一个由二维数组表示的矩阵，以及两个正整数r和c，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。

如果具有给定参数的reshape操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

示例 1:

1
2
3
4
5
6
7
输入:
nums =
[[1,2],
 [3,4]]
r = 1, c = 4
输出:
[[1,2,3,4]]

示例 2:

1
2
3
4
5
6
7
8
输入:
nums =
[[1,2],
 [3,4]]
r = 2, c = 4
输出:
[[1,2],
 [3,4]]

解题思路

1.蛮力法

将输入的数组nums先转换为一维数组，再将一维数组转换为二维数组

复杂度

  • 时间复杂度：O(m * n)
  • 空间复杂度：O(m * n)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int[][] matrixReshape(int[][] mat, int r, int c) {
        int total = mat.length * mat[0].length;
        if (total != r * c) {
            return mat;
        }

        int[] source = new int[total];
        int k = 0;
        for (int i = 0; i < mat.length; i++) {
            for (int j = 0; j < mat[0].length; j++) {
             source[k++] = mat[i][j];
            }
        }

        int[][] result = new int[r][c];
        k = 0;
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                result[i][j] = source[k++];
            }
        }

        return result;
    }
}

2.二维数组的一维表示

对于 $$ m×n $$ 的数组，映射为一维数组[0,mn)：

$$ (i,j) = i × n + j$$，

而对于一维数组中的x，映射到二维数组

$$ \begin{cases} i = x /n \ j = x % n \end{cases}$$ ，

剩下的思路和第一种方法一样，先转换为一维数组再变为二维数组

复杂度：

  • 时间复杂度：O(m * n)
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[][] matrixReshape(int[][] mat, int r, int c) {
        int m = mat.length;
        int n = mat[0].length;
        int total = m * n;
        if (total != r * c) {
            return mat;
        }

        int[][] result = new int[r][c];
        for(int x = 0; x < total; x++) {
            result[x / c][x % c] = mat[x / n][x % n];
        }

        return result;
    }
}

118. 杨辉三角

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

PascalTriangleAnimated2

在杨辉三角中，每个数是它左上方和右上方的数的和。

解题思路

根据图示可知，从第三行开始，除了第一列和最后一列，第i行第j列应该等于第i-1行的j-1 + j

复杂度：

  • 时间复杂度：O(numRows ^ 2)
  • 空间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> list = new ArrayList<>();

        for (int i = 0; i < numRows; i++) {
            List<Integer> innerList = new ArrayList<>();
            for (int j = 0; j < i + 1; j++) {
                if (j == 0) {
                    innerList.add(1);
                    continue;
                } else if (j == i) {
                    innerList.add(1);
                    continue;
                }
                innerList.add(list.get(i-1).get(j-1) + list.get(i-1).get(j));
            }
            list.add(innerList);
        }

        return list;
    }
}

387. 字符串中的第一个唯一字符

给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。

示例：

1
2
3
4
5
s = "leetcode"
返回 0

s = "loveleetcode"
返回 2

解题思路

二次遍历

第一次遍历记录s中的字符出现次数，第二次遍历返回较小的索引值

复杂度

  • 时间复杂度：O(n)，n 为s长度，遍历两次
  • 空间复杂度：O(1)，需要一个 26 个字母的字典

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int firstUniqChar(String s) {
        int[] table = new int[26];
        for(int i = 0; i < s.length(); i++) {
            table[s.charAt(i) - 'a']++;
        }

        for(int i = 0; i < s.length(); i++) {
            if (table[s.charAt(i) - 'a'] == 1) return i;
        }

        return -1;
    }
}

98. 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

  • 节点的左子树只包含小于当前节点的数。
  • 节点的右子树只包含大于当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

解题思路

1.递归

这道题容易出错的地方在于只根据当前节点判断左儿子和右儿子是否满足条件，忽略左子树中所有节点都必须小于当前节点，右子树中所有节点都必须大于当前节点。故设计一个函数isValid(root, lower, upper)，判断root的节点值是否满足lower < root.val < upper。

复杂度

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution{
    public boolean isValidBST(TreeNode root) {
        Long lower = Long.MIN_VALUE, upper = Long.MAX_VALUE;
        return isValid(root, lower, upper);
    }

    public boolean isValid(TreeNode root, long lower, long upper) {
        if (root == null) return true;
        if (root.val <= lower || root.val >= upper) return false;
        //对于左子树，上界是当前节点；对于右子树，下界是当前节点
        return isValid(root.left, lower, root.val) && isValid(root.right, root.val, upper);
    }
}

2.中序遍历

二叉搜索树的中序遍历是个有序序列，可以根据中序遍历判断该序列是否有序从而判断是否为二叉搜索树

复杂度

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution{
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        return inorder(root);
    }
    public boolean inorder(TreeNode root) {
        if (root == null) return true;
        boolean l = inorder(root.left);
        if (root.val <= pre) return false;
        pre = root.val;
        boolean r = inorder(root.right);
        return l && r;
    }
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution{
    public boolean isValidBST(TreeNode root) {
        LinkedList<TreeNode> stack = new LinkedList<>();
        long pre = Long.MIN_VALUE;

        while(!stack.isEmpty() || root != null) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (root.val <= pre) return false;
            pre = root.val;
            root = root.right;
        }
        return true;
    }
}

230. 二叉搜索树中第 K 小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

img

1
2
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

img

1
2
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

解题思路

**二叉搜索树(BST)**的特点：

  • 每个节点的左儿子比父节点小，右儿子比父节点大
  • 每个节点的左子树和右子树也是二叉搜索树
  • 二叉搜索树中序遍历的序列是一个升序序列

为了找到树中第K小的元素，可以按照中序遍历得到升序序列，第k-1个元素就是第k小的节点

采用迭代和递归两种方法实现

复杂度：

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

参考代码：

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution{
    public int kthSmallest(TreeNode root, int k) {
    	LinkedList<TreeNode> stack = new LinkedList<>();

        //中序遍历所有节点
        while (true) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            //弹出一个节点，k-1，当k等于0时节点值就是第k小的节点
            if (--k == 0) return root.val;
            root = root.right;
        }
    }
}

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    int res = 0;
    int rank = 0;
    public int kthSmallest(TreeNode root, int k) {
        traverse(root, k);
        return res;
    }

    public void traverse(TreeNode root, int k) {
        if (root == null) return ;
        traverse(root.left, k);
        rank++;
        if (rank == k) {
            res = root.val;
            return ;
        }
        traverse(root.right, k);
    }
}

538. 把二叉搜索树转换为累加树

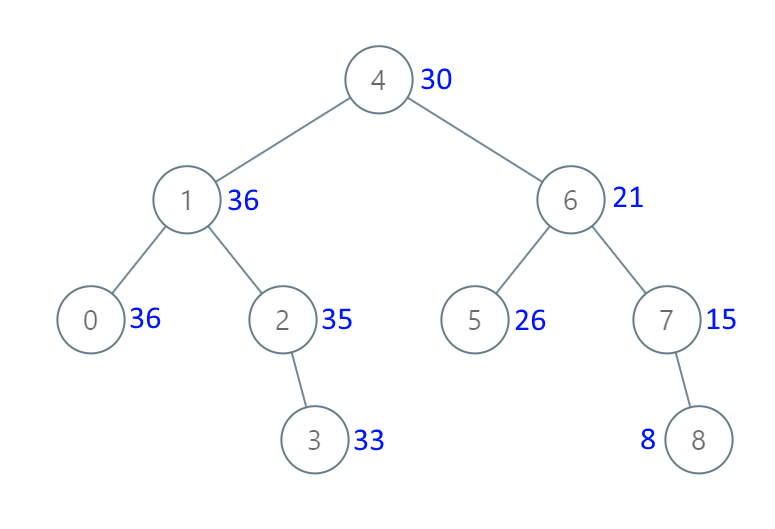
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

示例 1：

img

1
2
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

解题思路

反向遍历树，得到降序的序列，使用全局变量sum记录节点值

复杂度：

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution{
    public TreeNode convertBST(TreeNode root) {
        traverse(root);
        return root;
    }

    int sum = 0;
    public void traverse(TreeNode root) {
        if (root == null) return ;
        //反向遍历
        traverse(root.right);
        sum += root.val;
        root.val = sum;
        traverse(root.left);
    }
}

剑指 Offer II 024. 反转链表

给定单链表的头节点 head ，请反转链表，并返回反转后的链表的头节点。

示例 1：

img

1
2
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

解题思路

1.迭代

从链表头部开始一个一个改变next指针指向。操作过程如下：

  1. 保存当前节点的下一个节点
  2. 改变当前节点next指向前一个节点
  3. 向后移动当前节点
  4. 向后移动前一个节点

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public ListNode reverseList(ListNode head) {
	if (head == null || head.next == null) return head;
	ListNode pre = null;
	ListNode cur = head;
	ListNode nxt = cur;

	while (cur != null) {
		nxt = cur.next;
		cur.next = pre;
		pre = cur;
		cur = nxt;
	}
	return pre;
}

2.递归

参考代码：

1
2
3
4
5
6
7
public ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) return head;
    ListNode last = reverseList(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}

92. 反转链表 II

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

img

1
2
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

解题思路

  • 先找到反转开始节点leftNode，保存反转开始节点的前一个节点prev。
  • 反转[leftNode，rightNode]，保存rightNode的下一个节点next。
  • prev.next指向rightNode，leftNode.next指向next。
  • 返回头节点

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        //头节点可能会变化，定义伪头节点
        ListNode dummy = new ListNode();
        dummy.next = head;

        //找到leftNode
        ListNode leftNode = dummy.next;
        ListNode prev = dummy;
        for (int i = 1; i < left; i++) {
            prev = leftNode;
            leftNode = leftNode.next;
        }

        //反转链表
        ListNode pre = prev, cur = leftNode, nxt = cur;
        while (left <= right && cur != null) {
            nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
            left++;
        }
        ListNode next = cur;

        prev.next = pre;
        leftNode.next = next;

        return dummy.next;
    }
}

剑指 Offer II 027. 回文链表

给定一个链表的 头节点 head ，请判断其是否为回文链表。

如果一个链表是回文，那么链表节点序列从前往后看和从后往前看是相同的。

示例 1：

img

1
2
输入: head = [1,2,3,3,2,1]
输出: true

解题思路

1.快慢指针

先找到链表中间节点，对链表后半部分进行反转，再一一比较。

复杂度：

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)或者 O(1)，取决于使用递归还是迭代

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public boolean isPalindrome(ListNode head) {
	if (head.next == null || head == null) return true;
	ListNode fast = head.next;
	ListNode slow = head;

	while (fast.next != null && fast.next.next != null) {
		fast = fast.next.next;
		slow = slow.next;
	}
	ListNode mid = reverse(slow.next);
	while (mid != null) {
		if (head.val != mid.val) return false;
		mid = mid.next;
		head = head.next;
	}
	return true;
}

//递归反转链表
public ListNode reverse(ListNode head) {
	if (head.next == null) return head;
	ListNode ret = reverse(head.next);
	head.next.next = head;
	head.next = null;
	return ret;
}

剑指 Offer II 023. 两个链表的第一个重合节点

给定两个单链表的头节点 headA 和 headB ，请找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

img

解题思路

1.哈希集合

将单链表 A 中的节点放入集合中，遍历单链表 B 判断集合中是否存在相交节点

复杂度：

  • 时间复杂度：O(m+n)
  • 空间复杂度：O(m)

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
	Set<ListNode> set = new HashSet<>();
	while (headA != null) {
		set.add(headA);
		headA = headA.next;
	}
	while (headB != null) {
		if (set.contains(headB)) return headB;
		headB = headB.next;
	}
	return null;
}

2.双指针

定义两个指针pA和pB分别指向单链表 A 和 B 的头部。则会出现三种情况：

  1. 两个链表有交点，且 A 和 B 的头节点到交点步数相同

    image.png

    则易得pA和pB第一次遍历到达交点

  2. 两个链表有交点，但 A 和 B 的头节点到交点步数不同

    image.png

    当pA遍历完 A 链表后继续遍历 B，经过a+c+b步到达交点；同样的pB经过b+c+a步到达交点。

  3. 两个链表没有交点。

    image.png

    pA和pB最终都指向 null，但经过的步数也是相同的。

复杂度：

  • 时间复杂度：O(m+n)
  • 空间复杂度：O(1)

参考代码：

1
2
3
4
5
6
7
8
9
10
11
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
	ListNode pA = headA;
	ListNode pB = headB;

	while (pA != pB) {
		pA = pA == null ? headB : pA.next;
		pB = pB == null ? headA : pB.next;
	}

	return pA;
}

剑指 Offer 25. 合并两个排序的链表

输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。

示例 1：

1
2
输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

解题思路

使用伪头节点连接两个链表

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
	ListNode head = new ListNode();
	ListNode dummy = head;
	while (l1 != null && l2 != null) {
		if (l1.val > l2.val) {
			dummy.next = l2;
			l2 = l2.next;
		} else {
			dummy.next = l1;
			l1 = l1.next;
		}
		dummy = dummy.next;
	}

	if (l1 == null) {
		dummy.next = l2;
	} else {
		dummy.next = l1;
	}

	return head;
}

1171. 从链表中删去总和值为零的连续节点

给你一个链表的头节点 head，请你编写代码，反复删去链表中由 总和 值为 0 的连续节点组成的序列，直到不存在这样的序列为止。

删除完毕后，请你返回最终结果链表的头节点。

示例 1：

1
2
3
输入：head = [1,2,-3,3,1]
输出：[3,1]
提示：答案 [1,2,1] 也是正确的。

解题思路

定义两个指针pre和p，pre用于保存节点方便删除区间，p遍历链表找到前缀和为 0 的节点将其删去。

pre一开始指向伪头节点，只有当p走到结尾时才移动到下一个节点，而每当p走到前缀和sum=0时，更新pre的指向pre.next = p.next

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Solution{
    public ListNode removeZeroSumSublists(ListNode head) {
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode pre = dummy;

        while (pre != null) {
            //指针p指向pre后面的节点，计算前缀和
            ListNode p = pre.next;
            int sum = 0;
            while (p != null) {

                sum += p.val;
                //如果此时前缀和为0，删去(pre,p]区间的节点
                if (sum == 0) {
                    pre.next = p.next;
                    break;
                } else {
                    p = p.next;
                }
            }
            //当p走到结尾时，pre移动到下一个节点，否则不移动。
            if (p == null) pre = pre.next;
        }
        return dummy.next;
    }
}

232. 用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

解题思路

解题关键在于如何保证入队的元素插入到设计的结构的尾部即栈的底部，出队的元素在栈的顶部。

可以将一个栈设置为入队栈，入队元素都进入这个栈；另一个栈为出队栈。

  • 入队：入队栈直接push
  • 出队：当出队栈为空时，需要将入队栈中的元素一个一个pop到出队栈中，这样可以保证入队栈中最后进入的元素被push到出队栈的底部，最先进入的元素进入出队栈的头部；当出队栈不为空时，出队栈直接pop。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class MyQueue {
	Stack<Integer> inStack;
    Stack<Integer> outStack;

    public MyQueue() {
		inStack = new Stack<>();
        outStack = new Stack<>();
    }

    public void push(int x) {
		inStack.push(x);
    }

    public int pop() {
		if (outStack.isEmpty()) {
            while (!inStack.isEmpty()) {
                outStack.push(inStack.pop());
            }
        }
        return outStack.pop();
    }

    public int peek() {
		if (outStack.isEmpty()) {
            while (!inStack.isEmpty()) {
                outStack.push(inStack.pop());
            }
        }
        return outStack.peek();
    }

    public boolean empty() {
		return inStack.isEmpty() && outStack.isEmpty();
    }
}
上一页
2024-09-02 11:37:40 # 算法题 #leetcode #算法
下一页